In questo articolo ti dico che cosa sono i sottoinsiemi, analizzeremo il concetto di inclusione di una parte in un’altra più grande e vedremo alcuni esempi di sottoinsiemi.
Sottoinsieme o parte
Vediamo in dettaglio che cosa sono i sottoinsiemi; un insieme si dice {sottoinsieme (o parte)} di
quando tutti gli elementi di
sono contenuti in
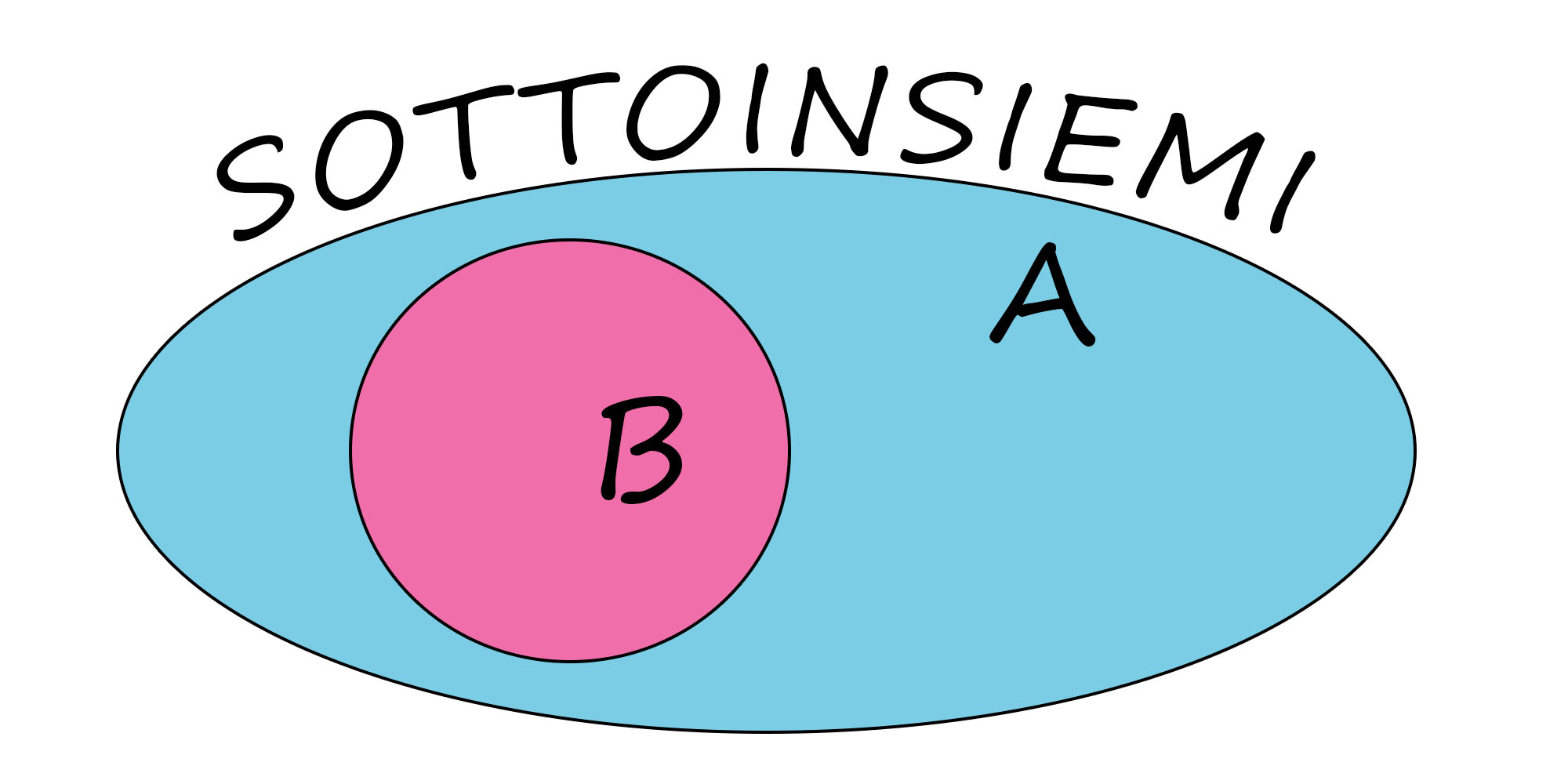
. Il sottoinsieme quindi, si può definire tale, quando è una parte di un altro insieme più grande. Quindi se
è contenuto in
,
Se almeno uno degli elementi di B non è contenuto in A, allora diremo che l’insieme B non è un sottoinsieme di A
{Sottoinsieme di se stesso}. Ogni insieme è un sottoinsieme di se stesso
{Sottoinsieme vuoto }. Si indica con lo zero tagliato ed è un sottoinsieme di qualsiasi altro insieme, l’insieme vuoto
è contenuto in ogni altro insieme per il semplice fatto che se cosi non fosse, dovrebbe esistere un elemento di
che non esiste negli altri insiemi, ma questo è impossibile perchè
non ha elementi in quanto è un insieme vuoto.
Se vuoi approfondire il concetto di inclusione ti consiglio di visitare questa pagina wikipedia.
Esempi di sottoinsiemi
{N} (1, 2, 3, 4, 5, …) sono contenuti nei numeri interi relativi \textbf {Z} (…, -2, -1, 0, 1, 2, …)
{Q} ( ) sono contenuti nei numeri reali \textbf {R}
Segui questi link che ti propongo se vuoi conoscere la teorie degli insiemi e gli insiemi finiti ed infiniti.